DC Kaynaklı Seri RC Devresi Analizi
Son güncellenme Nisan 2009
19 Aralık, 5 Aralık 2010, DC kaynaklı Seri RC Devresi
Merhaba arkadaşlar bu yazıda DC kaynaklı seri RC devrelerinin analizini yapmaya çalışacağız, genellikle kitaplara formül olarak düşülen denklemlerin aslında basit bir birinci mertebeden diferansiyel denklemin çözümünden türediğini göreceğiz.

RC devrelerinde adından da anlaşıldığı üzere ve yukarda da resmi görüldüğü üzere seri bağlı direnç ve kapasiteden oluşan bir devrenin davranışı incelenir. Biz bu basit devrenin analizinde devre analizinin en temel kanunlarından olan KVL yani kirchoff voltaj yasasını kullanacağız.
I yönünde bir KVL dönersek;
1)  olur. Burdaki I(t) t anında devrede dolaşan akım ve V(t) t anındaki kapasite gerilimidir.
olur. Burdaki I(t) t anında devrede dolaşan akım ve V(t) t anındaki kapasite gerilimidir.
Kapasitenin tanım denkleminin
Q= C. V olduğunu biliyoruz. Her iki tarafın t ye göre türevini aldığımızda:
dq/dt = C . dV(t)/dt olur. Yani t anındaki kapasite akımının voltajı cinsinden değeri:
I(t) = C . dV(t)/dt olur. Buna göre KVL den yazdığımız ilk eşitlik
2) – ε + C. dv(t)/dt . R + V(t) = 0 haline gelir.
kolaylık olması açısından dV(t)/dt ifadesi yerine V’ yazarsak eşitliğimiz:
3) C.R.V’ + V = ε haline gelir ki bu denklem görmeye alışık olduğumuz diferansiyel denklem modellerindendir; birinci mertebeden, doğrusal, homojen olmayan dif. denklem(first order linear non-homogen diff. equ.). Bu denklemi birinci mertebeden doğrusal diferansiyel denklem(first order linear dif. equ) olarak düşünüp çözebileceğimiz gibi(integral faktörü bularak) yüksek mertebeli diferansiyel denklem çözüm yöntemlerinden birini kullanarak da çözebiliriz. Tabi burada bir mesele de ε un yani devremizin kaynağının nasıl bir davranış gösterdiğidir. Kaynağımızın zamana bağlı değişim gösteriyor olup olmaması çözümümüzü değiştirecektir. Bu yazıda DC kaynaklı devreleri değerlendirdiğimiz için kaynağımızın DC olduğunu düşünerek 3 nolu denklemimizi çözelim.
Diferansiyel denklemimizin çözümünün Y=Yh + Yp şeklinde olduğunu biliyoruz. Burda Yh , V(t) nin geçici(transient response) tepkisi, Yp V(t) nin kalıcı(steady-state response) tepkisini göstermektedir.Çözümü bulduğumuzda t sonsuza giderken geçici etkinin ortadan kalktığını, kalıcı tepkinin devam ettiğini göreceğiz. Önce Yh i bulalım:
Yh:
C.R.V’ + V = 0
Geçici hal çözümümüzün aşağıdaki formda olduğunu biliyoruz, bulmamız gerekenler c1 ve r değeri.
V = c1 . e^(r* t)
V’ = c1 . r . e^(r*t) bu iki ifadeyi yukarda yerine yazdığımızda:
c1 . e^(r *t) [ C. R .r + 1 )]= 0 olur, bu durumda eşitliğin sağlanması için C.R.r = -1 olmalıdır.
r = – 1/ R.C bu durumda Yh (homojen kısmın çözümü):
Yh = c1. e^(-t/RC) olur.(c1 sabit bir sayıyı temsil ediyor, kapasite sığası C ile bir ilgisi yok, c1 değeri kapasitenin ilk voltajıyla ilgilidir)
Sıra Yp: ın çözümüne geldi, yöntem olarak bilinmeyen katsayılar yöntemi (method of undetermined coefficients) kullanabiliriz, zaten kaynağımız da sabit olduğu için işimiz oldukça kolay. Sağ tarafta 0. dereceden bir polinom gördüğüm için yöntem gereği önereceğim Yp= A olacaktır. Yerine yazıp A yı çektiğimizde(Yp‘ 0 olur ve Yp direkt ε a eşit olur)
Yp:
Yp = ε . Bu durumda genel çözümümüz Yh + Yp ve de orjinal denklemimize uyarlarsak;
V(t) = c1. e^(-t/RC) + ε olur. Burda c1 sabitini bilmiyoruz, bulabilmemiz için bir başlangıç değerine sahip olmamız gerekir( yani herhangi bir t anındaki V(t) yi biliyor olmalıyız ).
V(0) = V0 olarak bildiğimizi varsayalım, genelde 0 anındaki değer verilir veya bulunur.
V(0) = c1 + ε = V0 olacağından
c1 = V0 – ε olur. c1 i yerine yazdığımızda:
V(t) = (V0 – ε)* e^(-t/RC) + ε olduğunu buluruz. Böylece bu devrede kapasitemizin geriliminin zamana bağlı davranışını ifade etmiş olduk.
Şimdi de bu sonucu biraz yorumlamaya çalışalım:
t=0 anında kapasite gerilimimiz V(0), eşitliğimizde t yerine 0 yazarsak:
V(0) = (V0 – ε). e^(-0/RC) + ε = V0 – ε + ε = V0 bu sonuç bizi şaşırtmadı çünkü biz hesaplama yaparken kapasitenin 0 anında bir V0 gerilimine sahip olduğunu varsaymıştık. V0 gerilimimiz 0 da olabilir, yani kapasitemizin başlangıç gerilimi olmak zorunda değil.
V(t) nin gidişatına baktığımızda eksponensiyel azalmanın olduğu (V0 – ε) ifadesinin giderek etkisinin azalacağını ve t = sonsuz olduğunda sadece ε değerinin kalacağını görürüz, yani kapasitenin ε voltajına geldiğini görürüz . Nitekim t yerine 0 yazdığımız gibi sonsuz yazarsak V(sonsuz)=ε olduğunu görürüz. Anlaşıldığı üzere ekponensiyel kısım sadece bir süre etkisini gösterdikten sonra etkisini kaybedecek ve kapasite gerilimi -kaynak varlığını sürdürdüğü müddetçe- ε olarak kalacaktır. Ne kadar bir süre etkisini gösteriyor? Yukarda da söylediğimiz gibi ekponensiyel kısım ancak sonsuzda 0 olur ve etkisinin tamamen yitmesi için sonsuza kadar beklememiz gerekir 🙂 ancak 5RC kadar vakit geçtiğinde e-5RC/RC ifadesinin alacağı değer çok küçük olacağından 0 olduğu ve artık etki etmediği kabul edilir, yani sorumuzun cevabı 5*R*C saniyelik bir süre. Bu zaman miktarı aynı zamanda 5 zaman sabiti olarak adlandırılır, bir seri RC devresinde R*C çarpımı zaman sabiti olarak adlandırılır.
Sonuç: DC kaynaklı seri bir RC devresinde kapasite gerilimi-ilk değerinden bağımsız olarak- er-geç kaynağın dayattığı gerilime gelir, ne kadar geç geleceği yaklaşık 5*R*C çarpımı kadardır.
RC Zaman Sabiti:
RC zaman sabiti bir RC devresinde geçici hal tepkisinin ne kadar süreceği hakkında bilgi verir. Şöyle ki: X volta dolu bir C kapasitesi bir R direnci üzerinden Y volta boşaltılmak istenirse(Y=0 da olabilir) veya A volta dolmuş bir C kapasitesi bir R direnci üzerinden B volta doldurulmak istenirse bu işlemlerin herbiri 5*RC kadar zaman alacaktır. Örn: 2V a dolmuş 1 uF lık bir kapasiteyi 1k üzerinden 3Volta veya 30Volta veya 50Volta doldurmak istersek bu işlem için 5RC=5*(1/000000)*1000=5ms zaman geçecektir. Bu sürenin ilk ve son volt değerlerinden bağımsız olduğunu sadece R*C çarpımına bağlı olduğunu hatırlayınız.
“Zaman sabitinin birimi nasıl saniye olabilir? ” sorusu akıllara gelmiş olabilir, şöyle: kapasite tanım bağıntımız Q=C.V idi, bu durumda C nin birimi coulomb / V dir. RC nin birimi ise ohm*coulomb/V dir. Ohm/V nin 1/A (bir bölü amper) olduğunu ohm yasasından biliyoruz. Bu durumda RC nin birimi coulomb/A oldu. Akımın tanım bağıntısın dQ/dt olduğunu biliyoruz, yani akımın birimi aynı zamanda coulomb/t dir. Bu durumda RC nin birimi coulomb/(coulomb/t) olacağından RC miz saniye cinsinden bir değer olacaktır(akım bağıntısında dQ/dt deki Q coulomb t de saniye cinsindendir).
Hatırlayacağınız üzere V(t) nin ekponensiyel azalmanın olduğu kısmını ilk yazdığımız diferansiyel denklemin(3 nolu denklem) homojen çözümden; ε u bulduğumuz kısmı da diferansiyel denklemimizin particular(kısmi) çözümünden bulmuştuk. Homojen ve particular ifadeleri matematiksel ifadelerdir, bu ifadelerin devremizdeki karşılıkları ise sırasıyla, geçici ve sürekli hal tepkisi dir. Burda geçici hal: (V0 – ε). e-t/RC ifadesinden gelmekte, kalıcı hal ise ε ifadesinden gelmektedir. Şimdi isterseniz sonucumuzu görselleştirebilmek için kapasitemizin gerilimin zamana göre değişimini veren ifadenin yani V(t) = (V0 – ε). e-t/RC + ε matlab yardımıyla grafiğini çizelim.
Grafiğimizi çizdirmeden önce nasıl bir grafikle karşılaşırız sorusuna cevap aramakta fayda var.İlk durumda kapasitemizdeki gerilimin 0 olduğunu yani olmadığını düşünelim, her şeyden önce ilk değerimizin 0 ve son değerimizin ε olacağını denklemimize baktığımızda görebiliyoruz ve 5RC zamana kadar bir geçiş(artış) olacak(5RC zamandan sonra çok az bir artış sonsuza kadar devam edecek ancak biz o artışı ihmal ediyoruz) ve sonrasında kapasite gerilim ε olarak kalacaktır. Fiziksel yapısı gereği kapasite gerilimi hiç bir zaman sıçrama yapamaz yani ani bir şekilde 3V gibi bir gerilimden 5V gibi bir gerilime atlayamaz. Kapasite geriliminin ani değişememesi sebebiyledir ki kapasite elemanının durum değişkeni(state variable) voltajıdır, durum değişkeni herhangi bir sistemin durumuyla ilgili bize öz bir bilgi verir. Mesela bir kapasite elemanı üzerinde 4V luk gerlim varsa deriz ki demek ki bir kaynak bu kapasiteye bir süre uygulanmış ve gerilimi 4V a getirmiş. Kapasite belleği-hafızası- olan bir elemandır ve belleğinde voltaj değerini tutar. Eğer kapasitenin durum değişkenine akımıdır demeye kalkacak olursak aşağıda göreceğimiz gibi bir anda 0 A den 5 A gibi bir değere çıkabilen veya 5A den bağlantıyı açtığımızda bir anda 0A a düşebilen bir durum değişkeni bize ne ifade edebilir ki!
V0= 0, kaynağımız ε=10V, R=10k ohm C=0.1 uF (RC zaman sabitimiz= 10000ohm * 0.1 uF = 1 ms oldu)
Beraber çizdirelim, Matlab’ı açalım:
t=0:0.0001:10*0.001; %yazarak 0 dan 10 milisaniyeye kadar 100 değer oluşturalım.
%(5. ms de kapasitemizin hemen hemen dolacağını biliyoruz )
%Formülümüzü yazalım:
V=(0-10)*exp(-t/10^-3)+10;
%ve çizdirelim:
plot(t,V);
%Eksenlerimize isimlerini verelim:
xlabel('zaman(saniye)');
ylabel('Gerilim(V)');
grid
Dediğimizde grafiğimiz:

şeklinde çıkmış olmalı, görüldüğü gibi 5RC zamanda (5.ms) kapasitemiz hemen hemen dolmuş, ε=10V değerine ulaşmıştır. RC kadar zamanda kapasitemiziz %63 ü dolmuş olur, yani kapasitemiz 6,3 V a dolmuştur.(Bunu eşitliğimizde t yerine RC yazarak kolayca bulabiliriz) .
Neticeten kapasite olarak adlandırdığımız devre elemanımız nasıl davranıyor?
Uçları arasındaki gerlimi ani değişemiyor ancak geçirdiği akım ani-bir anda- değişebiliyor, nitekim devremize kaynağımızı bağlamadan önce akımı 0 iken bağladığımız anda ε/R değerine çıkıyor ve zamanla azalıyor ve sonra sıfır oluyor, 5RC zaman sonra gerilimi kendisini besleyen kaynakla aynı olacağı için akım duruyor, 0 oluyor, çünkü gerilim farkı kalmıyor. Şu cümle de doğrudur: Bir kapasiteye yüklendiği gerilimden farklı değerde bir DC kaynak uygulandığında ilk anda şiddetli bir akım akar kapasite gerilimi uygulanan gerilime yaklaştıkça akımın da şiddeti azalır.
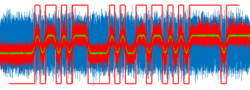
Şimdi de ani değişimli bir kaynağı(kare dalga üreten) RC devremize uygulayalım ve bakalım kapasitemizin gerilimi nasıl değişiyor:

Görüldüğü gibi kare dalgamız max değerine aniden çıkmasına rağmen kapasite gerilimimiz hemen yetişemiyor(5RC zaman gerekiyor) ve kare dalgamız 0 a düştüğünde de kapasite gerilimimiz hemen sıfıra düşemiyor. Peki kare dalgamızın periyodunu biraz arttırsaydık ne olurdu? Kapasite dolmak için yeterlli zamanı(5*R*C) bulacağından rahat rahat dolabilecekti. Seçtiğimiz örnek değerlere göre biliyoruz ki 5*R*C çarpımı 5ms, o zaman periyodu 20 ms seçelim bakalım ne oluyor:

Görüldüğü üzere kapasitemiz 10ms zaman içerisinde rahat rahat dolabiliyor(veya boşalıyor).
Kapasitemizin dolabilmesi(veya boşalabilmesi) için hiç zaman tanımayan 300us periyotlu kare dalga uygularsak:

Burda da görüldüğü üzere kapasite voltajımız neredeyse sabit kalıyor, çünkü dolabilmesi veya boşalabilmesi için süre yok.
Yukarıdaki denemelerimizden çıkaracağımız önemli bir sonuç da şudur ki: Kapasite elemanımız üzerine uygulanan AC gerilimin frekansı düştükçe(periyodu arttıkça) kapasitemiz bu gerilimi takip edebildiği için daha yüksek tepkinlik gösterir, yani varlığını daha iyi hissettirir. Frekans arttıkça kapasite elemanı varlığını hissettirememeye başlar, yani düz bir tel gibi davranmaya başlar. Yukarıda ikinci yaptığımız 300us periyodu biraz daha düşürecek olsaydık(frekansı arttırsaydık) artık kapasite uçlarında neredeyse tamamen DC bir değer okuyacaktık, bu DC değer de aslında uygulanan kare dalganın ortalama gerilimi olacaktı. Kapasite elemanının alternatif akımlı(AC) devrelerdeki davranışı başka şekilde analiz edilir ancak bu gibi yaklaşımlarla da mantıklı sonuçlar çıkarılabilir. Sitede RC alçak geçiren filtre yazısına bakabilirsiniz.
Bu yazıda yaptığımız analizlerin bize kalan bir diğer yegane pratik bilgisi de şudur: Bir kapasite ve bir direnç seri bağlı ve biz bu devreye A V büyüklüğünde DC bir gerilim uyguladık, ne kadar süre sonra kapasite gerilimimiz A V olur, cevap basit: 5*R*C kadar süre sonra. Peki, B V a dolmuş bir kapasitenin kaynak bağlantısını kesip bir R direnci üzerinden boşaltmak istiyoruz, ne kadar sürede boşalır, 0 V olur? 5*R*C sürede.
Kapasitemizin geriliminin zamana göre değişimini bir üstte çizdirdik, peki akımı? Yukarda ilk anda max olduğunu sonra 0 a kadar azaldığını söyledik. Şimdi de yine Matlab yardımıyla (yukarda verdiğimiz değerlerle) kapasitemizin akımının zaman göre değişimini çizdirelim.
Değerlerimiz şöyleydi:
V0= 0, kaynağımız ε=10V, R=10k ohm C=0.1 uF (RC zaman sabitimiz= 10000ohm * 0.1 uF = 1 ms oldu)
Bunun için önce akımın zaman bağlı değişimini veren ifadeyi bulalım.
Kapasitemizin akımının:
I(t) = C . dV(t)/dt olduğunu biliyoruz, o zaman önceden yazmış olduğumuz V(t) ifadesinin t ye göre bir defa türevini alıp C ile çarptığımızda i(t) ifadesini bulabiliriz.
V(t) miz
V=(0-10)*exp(-t/10^-3)+10 idi.
Bu durumda:
i(t)=C*-10*exp(-t/10^-3)/ (-1/10^-3) olur , yani:
i=0.1*10^-6*-10*exp(-t/10^-3)*(1/(-1/10^-3)) olur(ifade biraz karışık görünüyor ancak yaptığımız iş V(t) yi türetip C ile çarpmak).
i=0.1*10^-6*-10*exp(-t/10^-3)*(-1/10^-3) ifadesini matlaba verip t ye bağlı değişimini çizdirmek istediğimizde;
plot(t,i)
grid dediğimizde grafiğimiz:

şeklinde olur, görüldüğü gibi t=0 anında akımımız 10V/10k dan 10^-3 amper yani 10ma.
Akımımız 10 mA den başlayıp(0 anında 0 amperden 10 mA e ani bir çıkış var, demek ki kapasite akımı ani değişim gösterebiliyormuş.) 5RC saniye sonra -kapasite gerilimimiz 10V a ulaştığı için- 0 a düşüyor.
Sorular:
1) Başlangıçta boş olduğu bilinen 10uF lık bir kapasiteye 1k lık direnç üzerinden 9V luk bir kaynak bağlanmıştır. Kapasite 9V a ne kadar sürede dolar?
Cevap: 5*R*C =50ms
2) 9V a dolmuş C=100nF lık bir kapasiteye R=10k lık direnç üzerinden 5V luk bir kaynak bağlanmıştır, kapasitenin 5V a düşme süresi nedir?
Cevap: 5*R*C =5ms
3) Kapasitesi 10nF olan C1 kapasitesi ve kapasitesi 22nF olan C2 kapasitesi 10V a dolmuşlardır. Bu kapasitelerin yüzeylerinde bulundurdukları toplam pozitif yük miktarı nedir?
Q=C*V
Q1=100nC, Q2=220nC
şimdi baktım.bravo helal olsun.yubil de güzel.tebrikler böyle çalışan insanlara her daim ihtiyacımız var Allah kolylık versin
tebrik ederim çok iyi bir şekilde hazırlamışsınız yazıyı. sayenizde bir şeyler öğrendim bu konu hakkında çünkü derste hocalarımız ya tam açıklamıyorlardı ya da hızlı geçiyorlardı ama siz de bizim gibi bir öğrenci olduğunuz için aynı sorular oluşmuş olsaki kafamızda tam istediğim gibi anlatmışsınız. TEŞEKKÜRLER…
yazılarınız çok başarılı siteniz tam bir kaynak.teriyle pratiğin birleştiiği bilgiler bulunuyor. elinize sağlık gerçekten.başarılarınızın devamını dileriz..
çok teşekkür ederim ,sayenizde derste anlamadığım bu konuyu matlabda deneyerek öğrendim, allah razı olsun.
Müthiş bir çözümleme. Bu tür kaynak ancak konunun çeşitli boyutlarına vakıf bilim gönüllüleri tarafından hazırlanabilir. Bu tür kaynaklar Türkiye’nin geleceğini oluşturacak gençlere çok faydalı olacaktır. Eline sağlık…
rc devreleri nin kullanım alanları nelerdir acaba ?
Bu yazıda RC devresinin DC ile beslendiği durum incelenmek istendi. RC devresi en basit bir zamanlama devresidir. Hassasiyet gerektirmeyen zamanlama devrelerinde kullanılabilir.
RC devresine verilen bir DC değer belirli bir sürede kapasiteyi doldurur, kapasitenin belirli bir voltajı geçmesiyle röle tetikletebilirsiniz böylece bu süreyi zamanlama yapmak için kullanabilirsiniz. Mesela süreli yanan apartman lambaları, anahtara bastığınızda bir kapasiteyi küçük bir direnç üzerinden hemen doldurursunuz, anahtarı bıraktığınızda kapasite daha büyük bir dirençle toprağa bağlanır(belirli bir sürede boşalacak). Lamba, kapasite belirli bir voltajın altına düşmediği sürece yanacak bir devre ile kontrol edilir. Kapasitenin belirli voltajın altına düşme süresi değeri C ve seri bağlı olduğu R ye bağlıdır. Bu örnek şu anda düşündüğüm seri RC zamanlamanın kullanılabileceği olası bir uygulama.
Şu bağlantıya bakabilirsiniz:
http://www.screentoaster.com/watch/stUE5TQUNNRFtXSVtcWVNRUVJd/apartman_lambasi_rc_devresi_zamanlay_c
İyi çalışmalar.
Çok teşekkürler, iyi çalışmalar.
verdiğiniz bilgiler için çok teşekkürler rl devreleri hakkında bilginiz var mı acaba birde rl devreleri ile ilgili bir yazı yazarsanız ben ve benim gibi öğrenci kardeşlerim için çok faydalı olcanı düşünüyorum… emeğinize sağlık tekrar teşekkürler… bu arada sanırım videonuz silinmiş açılmadı….
Emeğinize sağlık teşekkürler.
mrblar bi konuda yardımınıza ihtiyacm var Vpp degeri=80v T=20ms olan seri rc devrisnde R=10kohm C=400nF ise t<0,0<=t<=10ms,10<=t<=20ms içn Vo(t) denklemini nasıl elde ederim ? [c üzerndeki gerilim Vo]
Vpp derken kaynak kare dalga mı sinüzoidal mi? Kare dalga ise sorunuzun cevabını bu yazıdaki bilgilerle bulabilirsiniz, sinüzoidal ise olay değişir. Kolay gelsin.
çok temiz ve sade notlar çok teşekkürler
Çok güzel bir anlatım, teşekkürler.
rc çarpımınn zaman boyutunda olduğunu nasıl açıklayabilirim ?
Yazının içinde açıklama var.
Hocam gerçekten mükemmel anlatım teşekkürler