Seri RC Devresinin Kare Dalga Cevabı
Son güncelleme: 1 Ocak 2013
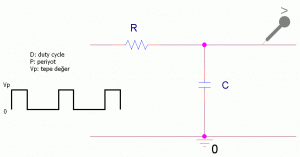
Seri RC devresinin kare dalga ile sürülmesi durumundaki sonuçları inceleyelim:
Periyoda P, “duty cycle” a ondalık olarak D dersek, kapasitemiz P*D süre şarj olmakta P*(1-D) süre deşarj olmaktadır. Şarj süreci sonunda kapasite voltajlarına V1, V2, V3 … Vn diyelim. Amacımız seri RC devremiz; tepe değeri, D si ve P si bilinen bir kare dalga ile sürüldüğünde herhangi bir n. adımda kapasitenin voltajını öğrenmek. Adımlarımız şarj süresi sonuna göre ayarlandı, bu değer bulunduktan sonra deşarj süresi sonundaki voltaj da kolayca bulunabilir. Sitede başka bir yazıda(bu sitenin ilk yazısı) C elemanının DC şartlardaki davranışına bakmıştık:
V(t) = (V0 – ε)* e^(-t/RC) + ε
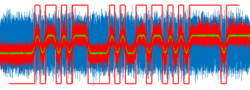
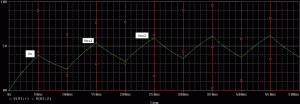
Burada V0 kapasitenin ilk değeri epsilon ise kaynak gerilimi idi, biz burada kare dalganın tepe değerini Vp ile temsil edeceğiz. Seri RC miz kare dalga ile sürüldüğünde ne olduğuna aşağıdaki iki grafikle devam edelim:
Art arda gelen iki şarj sürecinin sonunda voltajların aşağıdaki bağıntıyla değiştiği görülebilir(Yukarıda verilen V(t) ifadesinde epsilon ve V0 ı yerine yazdığımızda, V0 bir önceki voltajın deşarj sonrası değeri):
Vn=[Vn-1 *exp(-P*(1-D)/RC) ] * exp(-P*D/RC) + Vp* (1-exp(-PD/RC))
Bu ifade
Vn=a*Vn-1 + b olarak düşünülebilir, a ve b görülebileceği gibi hesaplanabilen sabit sayılardır.
a=exp(-P/RC)
b=Vp* (1-exp(-PD/RC))
Daha alışık olduğumuz gösterimle; iki şarj süresi sonucu oluşan ikinci voltaj öncekine:
f(x)=ax+b gibi bir fonksiyonla bağlıdır.
Burada merak ettiğimiz n. adımda yani f(n) (x)= ? ne olduğudur. Yerine yazmaya devam edersek:
fof(x)=a^2 x +ab + b
f(3) (x)=a^3 x + a^2 b + ab + b
…
f(n)(x)=a^n x + b*[1+a+a^2+a^3+…+a^(n-1)] olduğu görülür. |a|<1 olduğu durumda(bizim durum gibi) bu ifadenin:
f(n)(x)= a^n x + b*[1-a^(n+1)]/[1-a] ya eşit olduğu gösterilebilir(geometrik seri toplamı: 1-a^n / 1-a).
Burada x imiz Vn in ilk değeri, hatırlarsanız ilk değeri aldık ve n defa fonksiyona verdik. İlk değer sıfır kabul edilebilir, çözümde bir hata olmaz (itirazlar yorum bölümüne :)).
V(n)= b*[1-a^(n+1)]/[1-a] olarak yazılabilir.
Ripple voltaji türetilen ifadeden bulunabilir:
n arttıkça şarj sonrası gerilimin b/(1-a) ya yakınsadığı görülür [|a|<1].
Deşarj ile bu gerilimdeki değişim:
[b/(1-a) ] – [b/(1-a)]*exp(-P*(1-D)/RC) bu da
[b/(1-a) ] * [1-exp(-P*(1-D)/RC)] olacaktır.
Vripple=[b/(1-a) ] * [1-exp(-P*(1-D)/RC)]
Belirlenen bir ripple voltaj için min RC değerin belirlenmesinin analitik çözümü yapamadım, sadece D=0.5 özel durumu icin mümkün gibi görünmekte.
Bulduklarımızda ilgili sayısal örnekler(sonuçlar spice ile kontrol edildi):
R=1meg, C=100n, P=1ms, D=0.1 ve Vp=10V olan durumda çıkışın 1V a ulaştığı adımı bulunuz:
1=b*[1-a^(n+1)]/[1-a] ifadesi hesap makinesi ile elde veya mathcad ile çözülebilir:
R=125k, C=100n, P=1ms, D=0.5 ve Vp=5V olan durumda ripple voltajını bulunuz:
R=125k, C=100n, P=1ms, D=0.25 ve Vp=5V olan durumda ripple voltajını bulunuz:
Konunun başlangıcı ve asıl konuşulduğu yer:
http://www.picproje.org/index.php/topic,35164.0.html
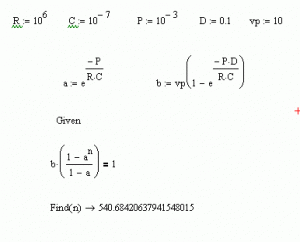

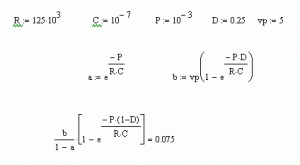
0 thoughts on “Seri RC Devresinin Kare Dalga Cevabı”