Faz Farkı

Fazörler (phasors)

Son güncellenme: 3 Haziran 2019, 2 Kasım 2011, 17 Kasım 2010, 24 Mayıs 2010.

Fazör (phasor), sinüzoidal işaret temsil eden karmaşık sayıdır (complex number, a+i b), sinüzoidal işaretleri fazör ile temsil ettiğimizde türevli ifadeler yerine kompleks çarpma/bölme işlemleri gelmektedir, sinüzoidal kaynaklı devrelerin sürekli hal tepkilerinin bulunması kolaylaşmaktadır.

Farklı kombinasyonda  bağlanmış R, L ve C elemanları bulunduran bir devrede f frekanslı sinüzoidal bir kaynak devrenin bir yanından devreyi sürmeye başlasın, bir süre sonra (devre sürekli hal durumuna geldiğinde, geçiş bölgesi bitip genlikler sabit bir değere oturduğunda) devredeki tüm akım ve gerilimler kaynağın dayattığı f frekanslı sinüzoidaller olur (Not1). Bu durumu gözünüzde canlandırın, her şey duruyordu, bir sinüzoidal kaynak devreyi f frekansında dürtüklemeye(!) başladı ve bir süre sonra devredeki tüm akım ve gerilimler kaynakla aynı frekanslı ancak farklı genlik ve fazda olarak kaynağa ayak uydurdu…  Sürekli hale geçmiş sinüzoidal kaynaklı bir devrede bu sinüzoidallerin genlik ve fazlarını bulmak için diferansiyel tanım/denklem gerekmemektedir. Diferansiyel tanım geneldir, her durumda geçerlidir (örneğin DC kaynaklı bir devrede) ancak sinüzoidal kaynaklı bir devrede akım ve gerilimler arasında basit tanımlar (kompleks cebirden faydalanılır) kullanarak devredeki tüm akım ve gerilimler bulunabilmektedir. Bu sinüzoidalleri karmaşık sayıyla temsil edilir (özel adı fazör), sinüzoidaller arasındaki tanım da karmaşık oranlarla (özel adı: empedans) ifade edilir. Burada karmaşık sayılar ve karmaşık cebir işimize yarıyor, kullanıyoruz.

Not1: f frekanslı iki sinüzoidalin toplamı yine f frekanslı bir sinüzoidal olur. f frekanslı sürülen ve non-linear eleman (örn diyot) bulundurmayan, linear elemanlarla kurulan (örn R, L ve C elemanları sinüzoidal kaynaklı bir devrede linear davranır) bir devrenin hiçbir noktasında (akım, gerilim fark etmez) f frekansından başka bir frekans görülmez.

Herhangi bir devrenin analizi için 3 tip denkleme ihtiyaç duyarız, bu denklemler:

1) Bir kapalı çevre boyunca gerilimlerin toplamı sıfırdır, Kirchoff Voltaj Yasası-KVY.
2) Bir düğüme gelen akımların toplamı sıfırdır, Kirchoff Akım Yasası-KAY.
3) Devre elemanlarının tanım bağıntıları
bilgileri kullanılarak elde edilir.
Sinüzoidal kaynaklı bir devrenin analizinde fazör bir kolaylıktır dedik, fazörü konuşmadan önce sinüzoidal kaynaklı bir devrenin zaman bölgesindeki çözümünü görelim daha sonra devremizi fazör kullanarak çözüm  yapacağız. Zaman çözümü daha zor olmakla beraber sürekli hale geçene kadarki akım ve gerilimleri de bulmamazı sağlar, fazör çözümü sadece dengeye gelmiş devrenin çözümünde yani sürekli hal tepkisinin bulunmasında kullanılabilir.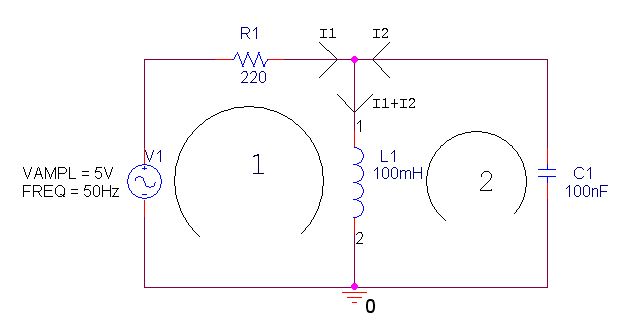

Yukarıdaki devrenin analizini zaman bölgesinde yapmak için I1, I2 akımlarını atayıp 1. ve 2.çevreden KVY(kirchoff voltaj yasası) yazarsak:
1. çevre için:

değerleri yerine yazarsak: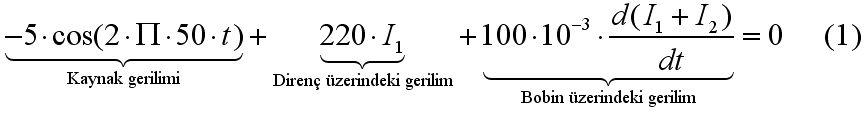

ve 2.çevre için değerleri yerine yazılmış şekilde: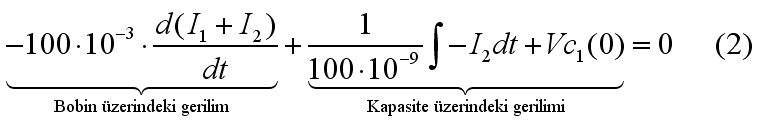

eşitliklerini elde ederiz.
2 bilinmeyen (I1,I2) ve 2 denklemimiz(1 ve 2) var, bu durumda I1 ve I2 yi bulabiliriz. Ancak karşımıza çıkan eşitlikler integrodiferansiyel denklem veya 2.dereceden diferansiyel denklem olacaktır. Çeşitli yöntemlerle bu denklemleri çözebiliriz ancak bu işlemler özellikle iki veya daha yüksek mertebeden devrelerde el ile çözüm için çok yorucu ve zor bir hal alır.

Sinüzoidal kaynaklı bir devrede(eğer doğrusal olmayan bir eleman yoksa) bütün akım ve gerilimler kaynakla aynı frekanslı sinüzoidal olur. Mesela bir kapasite elemanı üzerindeki akım veya gerilim, A kolundan akan akım veya B kolundaki indüktans üzerindeki gerilim, hepsi sinüzoidal ve kaynakla aynı frekanslıdır. Bu sinüzoidallerin frekansları kaynakla aynı farkları ise sadece genlikleri ve fazlarıdır. Bazısı diğerinden daha büyük genlikli, bazısı diğerinden faz olarak önde-geride. Tüm işaretlerin sinüzoidal olması ve devre elemanların tanım bağıntılarının sinüzoidal kaynaklı durumda türev yerine kompleks bir oranla tanımlanabiliyor olması devre analizimize bir basitlik getiriyor. Mesela, yukarıda saydığımız 3 tip denklem, özellikle 3. sü basitleşiyor:
1-2) Kapalı çevre boyunca gerilimleri toplamak veya bir düğüme gelen akımları toplamak sadece genlik ve faz bilgileri kullanarak yapılabilir. Örn: A*cos(wt+fi1) + B*cos(wt+fi2) toplamı birinci sinüzoidali A*exp(i*fi1) karmaşık sayısı ile temsil edersek(fazörünü yazarsak) ve ikinci sinüzoidali B*exp(fi2) karmaşık sayısıyla temsil edersek bu toplam A*exp(i*fi1)+B*exp(i*fi2) karmaşık sayılarının toplamının temsil ettiği sinüzoidaldir.

3) Asıl basitlik burda: Kapasite-indüktans elemanlarımızın tanım bağıntılarındaki türev veya integral işlemleri, devre kaynağı sinüzoidal olduğunda, sadece genlik ve faz değişimine sebep olduğundan tanım bağıntıları da basitleşiyor. Örn: İndüktans için gerilimin genliği akımın genliğinin w*L katı, gerilimin fazı akımın fazından 90 derece önde diyor çıkıyoruz işin içinden. Elemanımızın tanımı türevli bir ifadedense, genlik ve faz değişimi söyleyen basit bir ifade oldu. Empedans tanımında bu konunun üzerinden tekrar geçeceğiz. Görüldüğü üzere bize gereken 1-2-3 denklemlerimizin yeni ifadelerinde frekanstan hiç bahsetmedik, çünkü tüm büyüklükler aynı frekanslı, sinüzoidalleri bir kenara bırakıp sadece genlik ve faz bilgilerini tutuyoruz(fazör adı verdiğimiz bir karmaşık sayı ile).

Karmaşık sayıları(complex numbers) anlayalım:
Karmaşık sayılar iki boyutlu sayılardır. Kendi içerisinde tanımlı cebrik kuralları vardır. Toplama(çıkarma), çarpma(bölme) işlemleri tanımlanmış bir cebrik sistemtir. Bu iki boyutlu sayının bileşenleri; gerçek kısım ve sanal kısım olarak adlandırılır. Neden böyle adlandırılmış, karmaşık sayılar hayatımıza nasıl girmiş sorularının cevaplarından M.İdemen’in KDFT kitabının ilk bölümünde bahsedilmiş. Şu haliyle karmaşık sayı sistemi bizim için bir cebrik sistem. Nasıl ki reel sayılar cebrini veya boolean cebrini biliyorsak, karmaşık sayı cebri de kendi içinde kuralları tanımlanmış bir cebrik sistemdir. İşimize yarıyorsa kullanırız, yaramıyorsa kullanmayız. Biz burada kullanacağız çünkü karmaşık sayı cebrinde tanımlanan toplama ve çarpma(bölme) işlemleri sinüzoidal bir işaretin devrede maruz kalabileceği değişiklikleri tam ifade ediyor. Aynı frekanslı iki sinüzoidalin toplamının genlik ve fazı(düğüme gelen akımlar, çevre boyunca gerilimler toplamı); bu sinüzoidallerin genlik ve faz bilgilerini tutan karmaşık sayıların(fazörlerin) toplamıyla elde edilen kompleks sayının genlik ve fazına eşittir. İndüktans ve kapasitenin tanım bağıntısı da komplex bir çarpma(bölme) işlemiyle tam uyumludur.

Evet, kok(-1) fiziksel bir manaya karşı düşüremediğimiz bir sayıdır ancak bunun bir önemi yoktur. Karmaşık sayı cebrini anlamak ve elektronikte gönül rahatlığıyla kullanmak kok(-1) in manasında değildir. Elektronikte karmaşık sayılar, ya bir sinüzoidal işaret temsil etmek için(fazörler) ya da sinüzoidaller arasındaki ilişkileri(empedans/transfer fonksiyonu) ifade etmek için kullanılır.

Karmaşık sayılar kartezyen, kutupsal ve üssel(exponential) olarak 3 şekilde gösterilebilirler. j=kök(-1) ve (1/j)=-j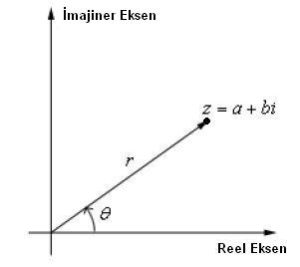


Sinüzoidal kaynaklı bir devrede bütün akım ve gerilimler yine sinüzoidaldir ve aynı frekanslı iki sinüzoidalin toplamı yine o frekansta bir sinüzoidaldir. Devredeki sinüzoidaller arasındaki fark sadece genlikleri ve faz farklarıdır. Fazör, bu sinüzoidal gerilim veya akımları genlik(tepe veya rms değeri) ve faz bilgilerini saklayarak temsil eden bir karmaşık sayıdır . Örn: A.cos(wt + ß ) işareti:

karmaşık sayısıyla temsil edilir(karmaşık sayı kutupsal[polar] koordinatlarda gösterildi). “A” değerinin tepe veya rms olması tamamen kabul meselesidir, ikisi de olabilir. Biz burda tepe değeri olan A olarak aldık, sinüzoidalin rms değeri olan A/kok(2) olarak da alabilirdik. Eğer RMS alsaydık bulduğumuz sonuçlar da RMS olacaktı, tepe değeri aldığımızdan bulduğumuz tüm fazörler tepe değer göstermektedir.
Fazörün sinüzoidal temsil eden bir karmaşık sayıdır, temsil edilmekle eşitlemeyi karıştırmayalım:

Örnek bir gerilim büyüklüğü için bu temsili şöyle yapıyoruz:
NOT: fazörleri ~ işareti ile belirteceğiz.

Empedans (Impedance)
Kapasite veya bobin elemanı sinüzoidal bir kaynakla sürüldüğü zaman akım-gerilim arasındaki ilişkiyi ifade etmek için aşağıda verilen türevli tanım bağıntılarını kullanmaya gerek yoktur:

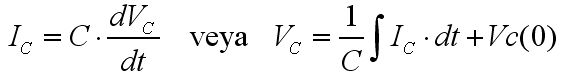
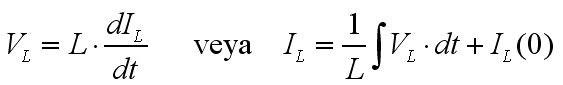
Bu eşitliklerin kapasite için Q=C*V ve bobin L*I=N*φ ifadelerinin bir kere zamana göre türetilmesinden geldiğini hatırlayınız.
Sinüzoidal kaynaklı devrelerin zaman bölgesinde analizinde karşımıza çıkan integrodiferansiyel veya diferansiyel denklemler bu elemanların tanım bağıntılarının diferansiyel içermelerinden ötürüdür. Analizi zorlaştıran yegane olay da budur.

Verilen tanım bağıntıları doğrudur ancak eğer bu elemanların sinüzoidal bir kaynakla sürüldüğünü biliyorsak bu bağıntıları daha kolay ifade edebiliriz. Nasıl mesela? Mesela diyebiliriz ki bobin elemanının gerilimi akımının w*L katı, gerilim fazı akım fazından 90 derece önde gidiyor(Burdaki w sinüzoidalin açısal frekansı, w=2*pi*f). Yerine yazalım doğru mu bakalım,  IL=sin(w*t) olsaydı gerilim ne oluyor? Gerilim: wL*cos(wt) oluyor, yani dediğimizde bir yanlışlık yok. Aynı şekilde kapasite elemanı için kapasite akımı, geriliminin w*C katı ve akım fazı gerlim fazından 90 derece önde gidiyor diyebiliriz. Görüldüğü üzere kaynağımın sinüzoidal olduğunu biliyorsam bu elemanların tanım bağıntılarını genlik ve faz değişimini söyleyerek ifade edebiliyorum. Genlik ve faz değişiminin sayısal ifadesi de bir karmaşık sayıdır, çünkü bir reel sayı sadece genlik değişimi söyleyebilir, dirençte olduğu gibi. Dolayısıyla bobin veya kapasite elemanımızın tanım bağıntısı (V/I eşitliği) bir karmaşık sayı ile söylenebilir, işte bu karmaşık sayıya empedans diyoruz. Karmaşık sayıları benimseyelim, iki boyutlu, kullanışlı yeni bir sayı olarak bakalım bu sayılara.
Kapasite ve bobin elemanı için empedans değerlerimiz:

Kapasite için:

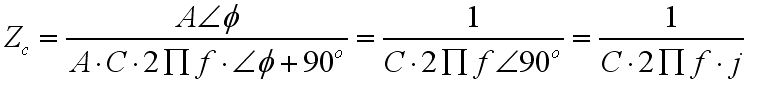
olur. [j = kök (-1)]
Aynı şekilde bobin elemanımızın empedansı: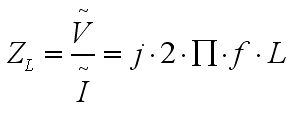

olur.

Böylece fazör bölgesinde kapasite tanım bağıntısı: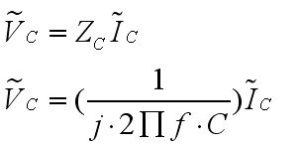

bobin tanım bağıntısı: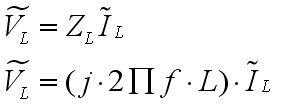

oldu.

Yani şimdi bobin elemanının tanım bağıntısına baktığımda iwL karmaşık sayısını gördüğümde(w=2*pi*f) anlıyorum ki genlik olarak gerilim akımın wL katı, V nin fazı I nın fazından 90 derece önde.

Ara not: Fazın önde-geride olması?
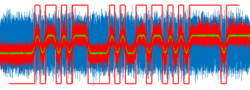
Bu aslında göreceli bir kavram, daire şeklinde bir pistte yarışan iki araçtan hangisi önde nasıl bilebiliriz? Arkada gibi görünen diğerine tur bindirmiş de olabilir:) Biz -iki aracı da içine alan- pistin yarısına bakıyoruz kim öndeyse o öndedir:) Devrelerimizde de iki sinüzoidalin tepe değerini gördüğü yarım periyoda bakıyoruz, kim önce tepe değeri aldıysa o öndedir. Matematiksel olarak cos(wt+fi), cost(wt) den fi derece öndedir fi<=180 derece için. Yani cos(wt+30), cos(wt+15) den 15 derece öndedir veya cost(wt+180), cos(wt) den 180 derece önde(tam ters işaretlisi) denebilir. cos(wt+181), cos(wt) den 179 derece geridedir 🙂 Aşağıdaki grafikte kırmızı veya mavi çerçeve alınmış rastgele seçilen yarım periyotluk dilimlerde tepe değeri dana önce gelen işaretin(kırmızı işaret) maviden fi kadar önde olduğu görülmektedir. fi=w*dt dir. Aynı frekanslı iki sinüzoidal arasındaki bu farka faz farkı diyoruz.
İndüktif yüklerde gerilimin akımdan önde, kapasitif yüklerde akımın gerilimden önde olduğunu biliyoruz. Tek indüktansın gerilimi, akımından 90 derece öndedir. Tek kapasitenin akımı, geriliminden 90 derece öndedir.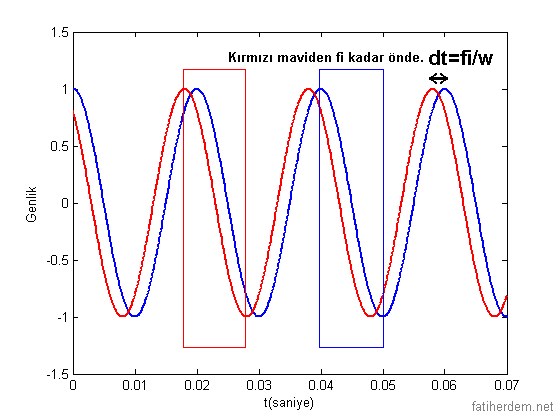

Görüldüğü üzere sinüzoidal işaretler için elemanımızın(kapasite veya bobin) tanım bağıntısı fazör bölgesinde daha kolay bir şekilde ifade edilebilir ya da bu tanım bağıntılarını daha kolay bir şekilde ifade ettiğimizde kendimizi fazör bölgesinde buluruz:). Fazör kavramının kullanışlılığı burdan kaynaklanır, bu elemanların tanım bağıntılarını kolaylaştırdığımızda integrodiferansiyel veya diferansiyel denklemler cebrik denklemlere dönüşür.Örnek devremizi fazör kullanarak analiz edelim: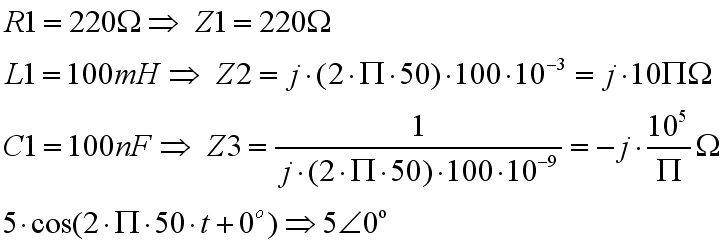

Kaynağımızın fazını 0 olarak kabul ediyoruz yani aslında devremizde kaynağımızı referans olarak alıyoruz. Kaynağımız cos ile ifade edildiyse herhangi çıkan bir sonucun “cosinus” bir işaret temsil ettiğiniz biliyoruz. Kaynağımıza sinus deseydik çıkan herhangi sonucun “sinus” işaret temsil ettiğini biliyoruz. Kaynağı referans alarak aslında biz fazör analizi sonucunda bulduğumuz tüm fazları kaynağa göre söyleriz, atıyorum R1 direncinin geriliminin genliği A fazı 30 bulundu ise kaynaktan 30 derece önde olduğunu anlarız. Örneklerde daha iyi anlaşılacaktır.
Devremiz fazör bölgesinde: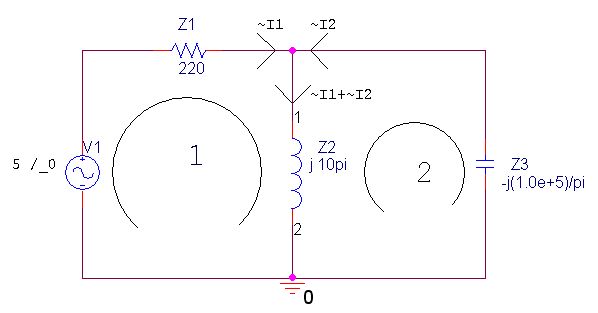

1. ve 2. çevreden: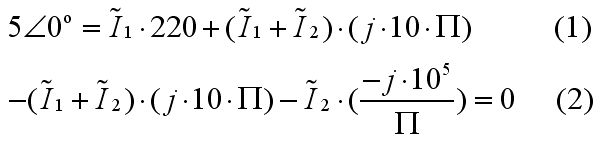

Denklemlerimizi düzenlersek: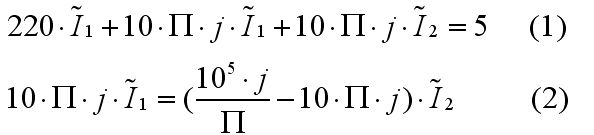


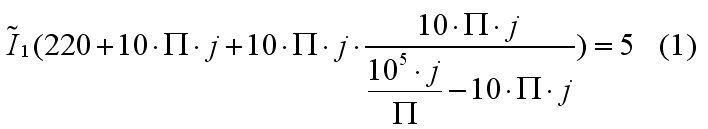
İşlemler Matlab de veya karmaşık sayı desteği olan bir hesap makinesinde yapılabilir.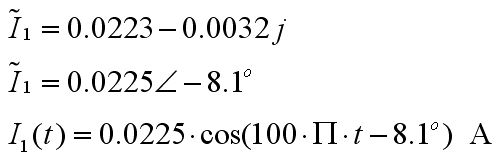

böylelikle I1 akımını bulduk. 2 nolu denklemden I2 yi de bulabiliriz.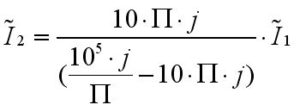


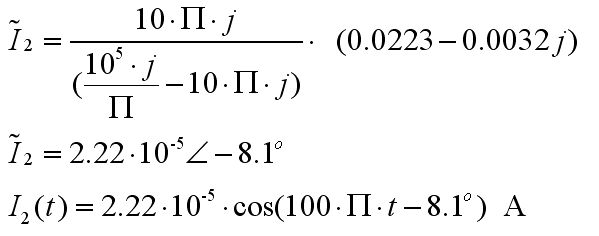
Böylelikle I1 ve I2 akımlarını bulmuş olduk. Sonuçlarımıza bakarsak I1 ve I2 akımlarının fazlarının aynı olduğunu görüyoruz(yuvarlatılmış haliyle) ve I1 akımının I2 akımına kıyasla yaklaşık 1000 kat daha büyük olduğunu görüyoruz. Bunu şöyle yorumlayabiliriz: Z2 ve Z3 empedanslarını bulmuştuk, Z3 empedansı Z2 ye kıyasla 1000 kat daha büyüktü dolayısıyla Z2 üzerinden akan akım Z3 üzerinden akana kıyasla 1000 kat daha büyük oldu. R direncinden geçen akımın çok büyük bir kısmı Z2 üzerinden akıyor, Z3 üzerinden ise çok az akım akıyor. R direncinden sağ tarafa baktığımızda neredeyse tamamen indüktif bir yük görüyoruz(seçtiğimiz L ve C değerlerinden ötürü). Kaynağımızdan sağ tarafa baktığımızda 220 ohm luk saf bir direncimize Z2//Z3 empedansının seri bağlandığını görüyoruz. Z1//Z2 ~ = Z2 çünkü Z2 empedansı Z1 e kıyasla çok küçük, dolayısıyla kaynağın gördüğü yük 220+Z2 o da 220 + 31.4j, yani kaynağımız hemen hemen rezistif bir yük görüyor, dolayısıyla I1 akımının faz kayması çok değil, sadece -8 derece. I1 akımında negatif işaretli bir faz kayması var(akım geride) çünkü yükümüz indüktif özellik gösteriyor.

Peki bizden indüktör(bobin) üzerindeki gerilim istenmiş olsaydı ne yapacaktık? I1 ve I2 fazör akımlarını bulmuştuk. İndüktör üzerindeki fazör gerilimi: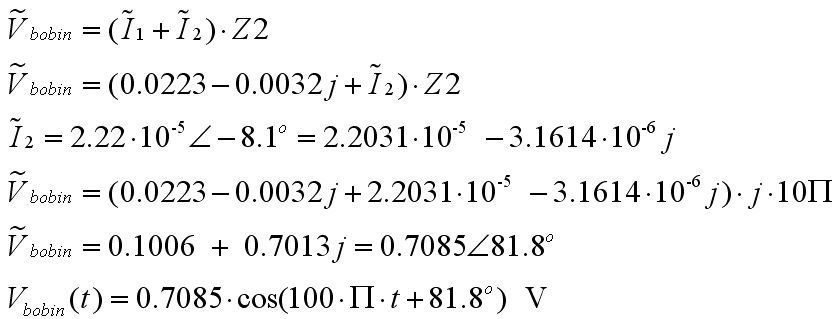

Böylece devremizin analinizi bitirmiş olduk ancak bulduğumuz sonuçların sürekli hal tepkileri olduğunu unutmayalım.

Devre analizinde gördüğümüz bir karmaşık sayı ne anlam ifade eder, gerçek hayatta imajiner bir büyüklük yoktur?
– Bir sinüzoidal işaret(akım veya gerilim) temsil eder efendim, büyüklüğü bu karmaşık sayının büyüklüğü ve fazı bu karmaşık sayının açısı olan bir sinüzoidal işaret temsil eder. L ve C elemanlarında olduğu gibi empedans değerlerinin karmaşık sayı olabileceğini unutmayalım. Örnekler(tüm açılar derece cinsinden):
Fazör 10j akımı 10.cos(wt+90) akımını temsil eder. (cos veya sin olması seçime bağlıydı, hatırlayınız.)
Fazör 3+4j gerilimi 5.cos(wt+53) gerilimini temsil eder. Karmaşık sayının formatı değişince aklımız karışmasın, sayının formatı yaptığımız işlemi kolaylaştırması için başka formlarda gösterilebilir(topl-çıkarma kartezyen, çarpma bölme polar formda daha kolay yapılır):
Fazör 20*exp(-45j) akımı 20*cos(wt-45) akımını temsil eder.
Zamanda bölgesinde100*cos(wt+30) akımını fazör bölgesinde 100*exp(30j) temsil eder.

*Çoğu analizde burda fazör kullandık denilmez, belki fazör bölgesine geçersek denir veya fazör karşılıkları direkt yazılır. Karmaşık sayıları görünce fazör olduğunu bizim düşünmemiz gerekir.

*İnternette veya bir kitap sayfasında herhangi bir akımın 100j olduğundan bahsediliyor mesela… aklımıza hemen genliği 100 V, fazı +90 derece olan bir sinüzoidal gelmelidir. Tek başına faz bilgisinin bir şey ifade etmediğini unutmayınız, bir faz bilgisi varsa muhakkak referans alınan bir kaynak sinüzoidal vs. olmak zorundadır. Neye göre +90 derece…?

Örnek Devreler:
1)Seri RC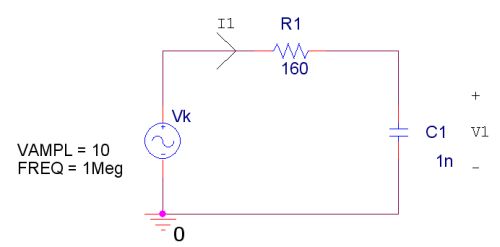

Vk=10.cos(2*pi*1000000*t) olmak üzere yukarıdaki devrede I1 ve V1 in sürekli hal tepkilerini bulunuz.

Çözüm:
Devremizi fazör bölgesine alalım: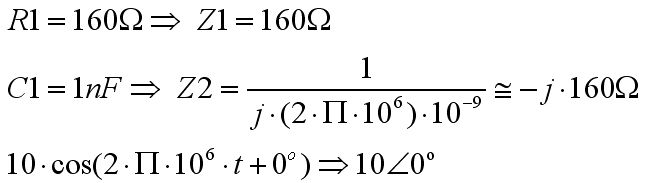

Bir KVY dönersek: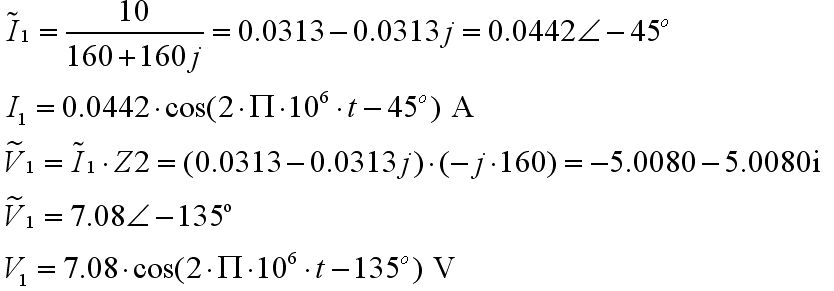

2)Paralel LC Rezonans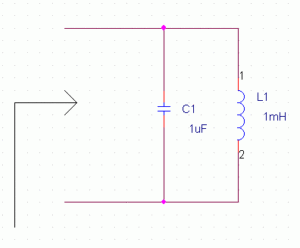

Yukarıdaki gibi paralel L-C devrelerinde ok yönünde bakıldığında görülen empedans bir f frekansında sonsuz olmaktadır(açık devre), bu frekansa paralel LC devresinin rezonans frekansı denir. Buna göre yukarıda verilen değerlere göre devrenin rezonans frekansını bulunuz.

Ok yönünde bakıldığında gördüğümüz empedansa Z, C ve L nin empedanslarına Z1 ve Z2 dersek:

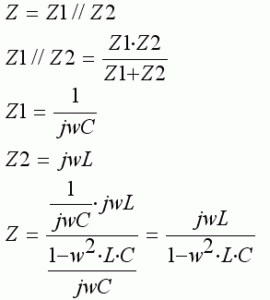
Bu empedansın sonsuz olması için paydanın sıfır olması gerekir.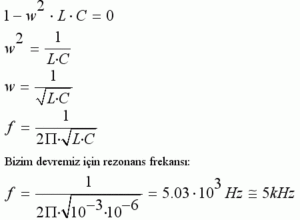

Bu yapı pratikte filtre tasarımında kullanılır. Yukarıdaki paralel rezonans devresine seri bağlı bir R direnci düşünelim. Oluşan devre bir bant geçiren filtredir. Bu devre rezonans frekansında girişindeki işareti aynen geçirecektir(çünkü açık devre). Eğer merkez frekansı 1MHz lik bir bant geçiren filtre tasarlamak istiyorsak rezonans frekansı 1MHz olan bir paralel L-C rezonans devresi kullanabiliriz. R yi neye göre seçeceğiz? R değeri filtremizin Q sunu, diğer bir ifadeyle filtremizin bant genişliğin belirler. R yükseldikçe filtremiz sadece rezonans frekansını geçirmek ister.