Taylor Serisi üzerine
Taylor serileri… Çok konuşulurdu ama ben ne olduğunu ne işe yaradığını pek anlamazdım. Taylor seri açılımı? x=c etrafında seri açılım… Neydi, ne işe yarardı … Sonradan anladım ki Taylor serileri fonksiyonların polinom şeklinde gösterilmesine yarıyormuş. Özellikle transcendantal fonksiyonlar olarak bilinen exp(x), sin(x), log(x) gibi fonksiyonların polinom olarak gösterilebilmesinde işe yarıyormuş. Bu gibi fonksiyonları çeşitli uygulamalarda polinom toplamı olarak göre göre bir şeyler çark etti.
Mesela exp(x) ifadesinin -eğer mümkünse?- 1+ x + 0.5*x^2+ … olarak yazılabilmesi bize değişik şeyler anlatıyor. Anlattığı şeylerden bir tanesini yazının sonunda konuşacağız.
Taylor serilerini anlamak/anlatmak için en güçlü argümanımı sunuyorum:
exp(x) örneğinden devam edelim, sorumuz şu: Acaba exp(x) fonksiyonu a+b x+c x^2+d x^3+e x^4+… şeklinde bir polinom olarak gösterilebilir mi?
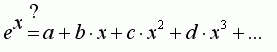
Olur mu olmaz mı hiç fikrimiz olmasın.
Varsayalım ki mümkün olsun, bu durumda a ne olurdu sizce? 0, 1, 100 …?
Eşitliğin her iki tarafında x=0 yazarsak a nın 1 olacağını görürüz. b, c, d… nin ne olduğuyla ilgili henüz hiç fikrimiz yok. Sadece a=1 in de exp(x) e pek benzer yanı yok:
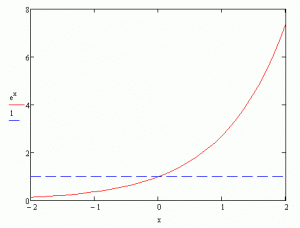
b, c, d… katsayılarından bize bir ekmek çıkması lazım;) yoksa kimseyi 1 in exp(x) olduğuna inandıramayız.
b yi bulabilmek için eşitliğin her iki tarafının türevini alıyoruz ve karşımıza:
exp(x)=b+2cx+3dx^2… ifadesi çıkıyor. Yine x=0 numarasını kullanarak b yi de buluyoruz.
b de 1 çıktı.
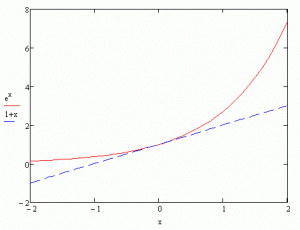
1+x ifadesinin, 1 e göre exp(x) e daha çok benzediği söylenebilir:
Ümitlendik, her iki tarafın bir defa daha türevini alarak c yi bulmak istiyoruz:
exp(x)=2c+6dx+…
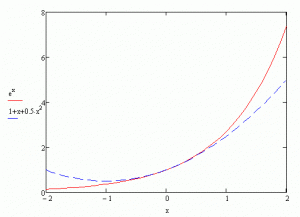
x=0 yazarak c yi 0.5 olarak bulduk. 3 terimli polinomumuzla exp(x) i karşılaştırıyoruz:
Vay be! Bu iş olacak gibi. Eşitliğin her iki tarafının türevini almaya devam ederek d, e, f … katsayılarını bulduğumuzda exp(x) e daha da çok yaklaşıyoruz. Şimdilik sadece -2 ile 2 arasında kıyaslama yapıyoruz, görünmeyen taraflarda hâlâ çok fark var ancak terim ekledikçe bu fark da azalıyor. Polinomumuz, asıl fonksiyona etrafında açılım yaptığımız noktadan itibaren yaklaşıyor. Sonuçta exp(x) fonksiyonunun x=0 da Taylor seri açılımı:
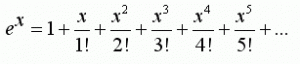
olarak bulunabilir.
Taylor seri açılımı her dereceden türevi alınabilen herhangi bir fonksiyonun polinom olarak gösterilmesini sağlayan bir olay.
exp(x)=1+ax+bx^2+… demiştik peki sizce
exp(x)=a+b*(x-1)+c*(x-1)^2+… şeklinde de gösterilebilir mi? Eşitliği sağlayan a, b, c… katsayılarını bulabilir miyiz?
x=1 yazarsak a=e, bir defa türetip tekrar x=1 yazdığımızda b=e, .. c=e/2… buldukça x=1 civarından başlayarak polinom exp(x) fonksiyonuna benzeyecektir. Bu 2. gösterim de exp(x) fonksiyonunun x=1 etrafında taylor s. açılımı olarak adlandırılıyor. Herhangi x=c etrafında açılabilir yeter ki açmak istediğimiz fonksiyon x=c etrafında her dereceden türevi alınabilsin. X=0 etrafında yapılan açılımın özel adı Maclaurin seri açılımıdır, Taylor serisinin özel bir halidir, ona da Taylor serisi diyebiliriz.
Taylor serisinden anlayabildiğim bu, bu olayın işe yaradığı başka bir olay, uygulama vs var mı? Var. Hem de güzel bir uygulaması var.
Teknik alanların hepsinde illa ki matematik var ama haberleşme teorisi ve elektroniği, matematik ile fiziksel dünyanın iyice kaynaştığı iki alan. Al defterden koy devreye, al devreden koy deftere desek yeridir. Haberleşmenin en temel olayı modülasyon işlemi, en temel modülasyon işlemi de DSBSC-AM denilen iki işaretin direkt çarpılması ile yapılan modülasyondur, buradaki çarpma bildiğimiz 6*8=48 çarpması gibi bir çarpma. m(t) mesajı ile sin(2*pi*1M*t) taşıyıcısının çarpılması işlemi mesela… Nasıl? Sorunun cevabı bir mixer ile çarpmak ama mixer nasıl çarpar?
Uygulamamızın öznesi diyot-mixer. Diyot mixer, basit bir diyot ile yapılan mixer. Burada odaklanacağımız olay diyot IV ilişkisindeki exp fonksiyonu.
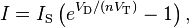 [wikipedia]. İfadede exp görüyoruz… şu polinom açılımının mümkün olduğunu yukarıda görmüş olduğumuz exp fonksiyonu. Yani diyotun transfer karakteristiğinde exp yerine 1+(Vd/K)+(Vd/K)^2+… şeklinde açılımı da yazılabilir.
[wikipedia]. İfadede exp görüyoruz… şu polinom açılımının mümkün olduğunu yukarıda görmüş olduğumuz exp fonksiyonu. Yani diyotun transfer karakteristiğinde exp yerine 1+(Vd/K)+(Vd/K)^2+… şeklinde açılımı da yazılabilir.
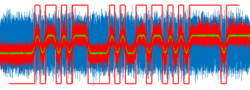
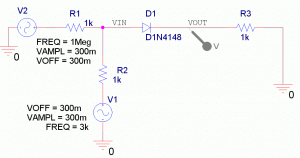
Allah Allah! Diyot, üzerine uygulanan gerilimin karesini de mi alıyormuş, küpünü, 4. kuvvetini… Peki m(t)+c(t) işaretini uygularsam karesinin alındığı yerde (m(t)+c(t))^2 ifadesinden m(t)^2+c(t)^2+2*m(t)*c(t) olacağından 2*m(t)*c(t) den çarpımı görecek miyiz? Evet, görüyoruz. Bu şekilde m(t) ve sin(2*pi*1M*t) yi çarpabilecek miyiz? Evet. PSpice da görelim. Daha gerçekçi bir mixer olması için iki işaretin toplamını süperpozisyon prensibinden elde edeceğiz, simülasyon ortamında iki sin kaynağını arka arkaya bağlayarak da toplayabilirdik.
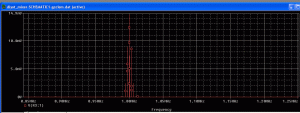
Evet basit bir diyot mixerimiz oldu, 1M etrafında x^2, x^3 terimlerinden gelen çarpımları görüyoruz. Giriş işaretlerinin offset değerleri değiştirilerek x^3 den gelen çarpım -third order product- azaltılabiliyor, bu örnekte diyodun sinüzoidal iki işareti çarpabildiği görülmek istendi.
Taylor seri açılımı aynı zamanda exp(i*x)=cos(x)+i*sin(x) eşitliğinin ispatlanmasında kullanılabilecek bir yöntem. Bu eşitlikteki terimlerin açılımlarını yaptığımızda eşitlik görülmektedir:
exp(ix)=1+ix+-0.5x^2+
cos(x)=1+0x-0.5x^2+…
i*sin(x)=0+ix+0+…
Yazıyı burada bitiriyoruz, çalışma isteğiniz-hevesiniz daim olsun. Selametle.
Bakılası ilgili kaynaklar:
http://en.wikipedia.org/wiki/Taylor_series
Math works 😉
Güzel bir yazı olmuş teşekkürler.Arif hocamız çok iyi anlattıgı için dersi alırken olayı az çok anlamıştım.Hesap makinelerinde de bu mantıkla hesaplamalar yapılıyor.
Gerçekten Calculus dersi alırken ne işime yarayacak dediğim herşeyi açıklamışsınız :)) Çok teşekkürler..
teşekkürler gerçekten çok iyi bir anlatım olmş
Bütün yazılara baktıkça daha hayran oluyorum.
Sen yaz gençlik zamanla okuyup anlar.
Helal sana…
Recai hocam iyi dileklerinize layık olabilmek isterim. Selamlar.
sempatik bir anlatım olmuş
Kolay gelsin burgers difüzyon denkleminin taylor seri açılımına göre çözümüyle ilgili yardımcı olabilir misiniz?
Merhaba, bilmediğim için yardımcı olamaycağım. İyi çalışmalar.
Bir matematikçi olarak anlatımınızı ve örneklemelerinizi çok beğendim. Ağzınıza sağlık, teşekkürler.
ya gerçekten güzelmiş.ellerine sağlık.beynimde ur gibi olmuştu artık.heryerden taylor lafını duyuyosun ama ne olduğunu bilmiyorsun..::)
Herzaman demişimdir ” konuyu anlatmadan önce işin hikaye kısmına mutlaka yer vermek gerekir ” diye. Ve siz bu işi gayet iyi yapmışsınız hocam. Emeğinize sağlık.
Elinize sağlık hocam.